How To Find The Midsegment Of A Trapezoid
Midsegments of trapezoids

A trapezoid's midsegment connects its non-parallel sides
The midsegment of a trapezoid is a segment that connects the midpoints of the two non-parallel sides of a trapezoid.

Howdy! I'chiliad krista.
I create online courses to help yous stone your math class. Read more.
If ???\overline{AB}\parallel\overline{DC}???, if ???F??? is the midpoint of ???\overline{Advertizement}???, and if ???Eastward??? is the midpoint of ???\overline{BC}???, then ???\overline{Atomic number 26}??? is the midsegment of the trapezoid.
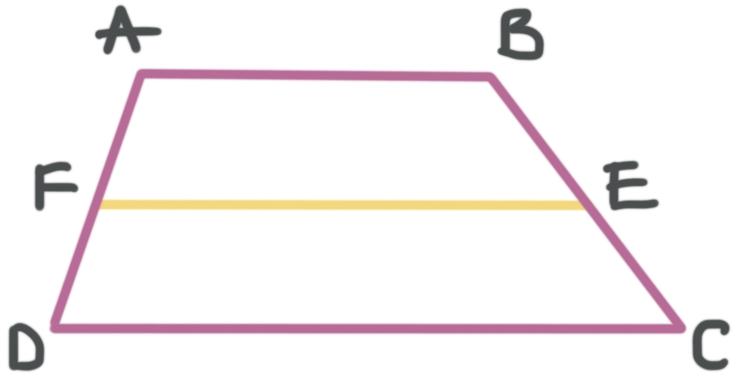
The human relationship between the length of the midsegment and the lengths of the parallel sides is
???Iron=\frac{ane}{ii}(AB+DC)???
The length of the midsegment of a trapezoid is always equal to one-half of the sum of the lengths of the parallel sides.
How to utilize the midsegment of a trapezoid to solve issues


Take the course
Want to learn more about Geometry? I accept a step-by-footstep form for that. :)
Finding the length of the side of the trapezoid, given the length of its midsegment
Example
In the trapezoid pictured, ???\overline{TU}\parallel\overline{WV}???, ???X??? is the midpoint of ???\overline{TW}???, and ???Y??? is the midpoint of ???\overline{UV}???. What is the length of ???\overline{WV}????
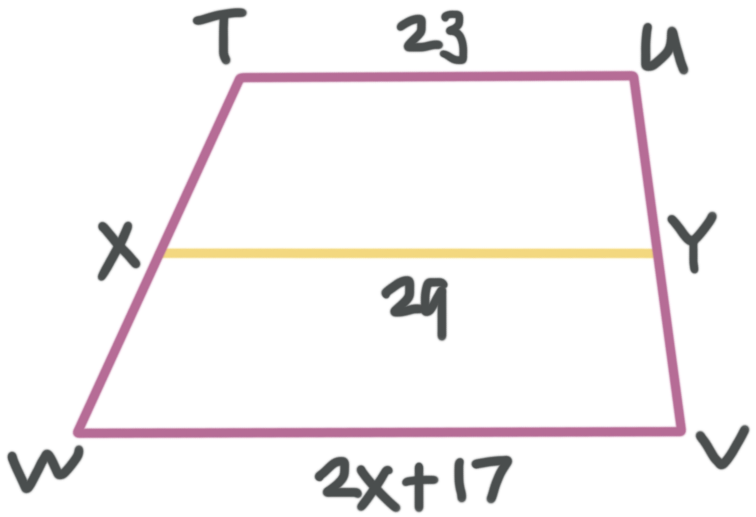
By definition, ???\overline{XY}??? is the midsegment of the trapezoid. Therefore, nosotros know that
???XY=\frac{1}{2}(TU+WV)???
Let'due south plug in what we know and then solve for ???x???.
???29=\frac{1}{2}(23+2x+17)???
???29=\frac{1}{ii}(40+2x)???
???29=20+10???
???nine=x???
So the length of ???\overline{WV}??? is
???WV=2x+17???
???WV=two(9)+17???
???WV=35???

The midsegment of a trapezoid is a segment that connects the midpoints of the 2 non-parallel sides of a trapezoid.
Instance
In the coordinate aeroplane, a trapezoid ???XYWZ??? has vertices at ???X=(-ii,2)???, ???Y=(3,2)???, ???Z=(-iii,-ii)???, and ???W=(4,-two)???. What is the length of the midsegment along the ???x???-centrality?
You tin plot the trapezoid and discover the lengths of the parallel sides.
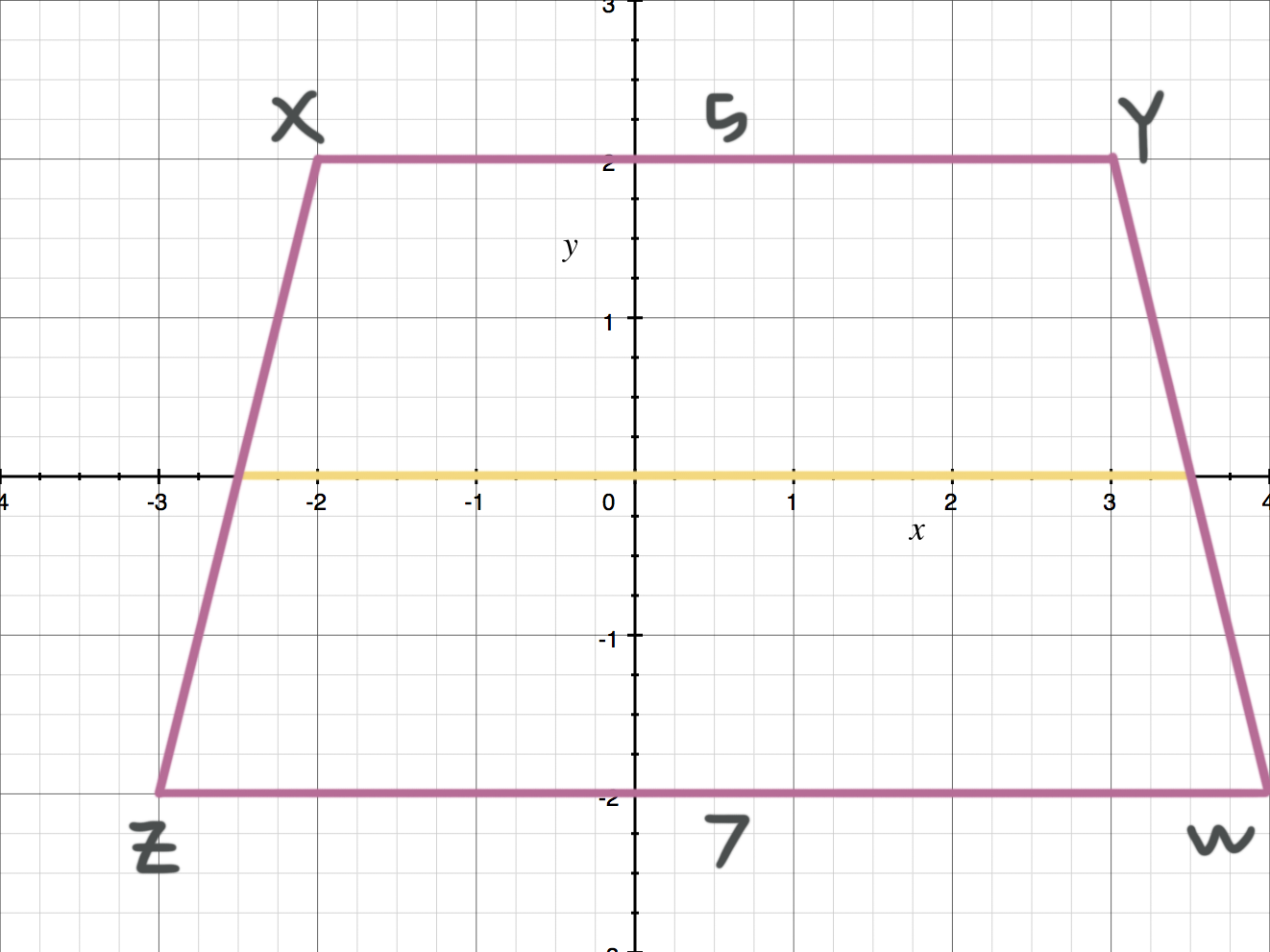
Remember the length of the midsegment is equal to half of the sum of the parallel sides, so the length of the midsegment is
???\frac{i}{ii}(XY+ZW)???
???\frac{1}{ii}(v+vii)???
???\frac{i}{ii}(12)???
???half-dozen???

Get access to the complete Geometry course
Source: https://www.kristakingmath.com/blog/midsegments-of-trapezoids
Posted by: greensupoed.blogspot.com


0 Response to "How To Find The Midsegment Of A Trapezoid"
Post a Comment