How To Find Current Across A Resistor In Parallel

6.ii Resistors in Serial and Parallel

LEARNING OBJECTIVES

By the finish of the section, you volition be able to:

Define the term equivalent resistance
Summate the equivalent resistance of resistors continued in serial
Summate the equivalent resistance of resistors connected in parallel

In Current and Resistance, we described the term 'resistance' and explained the basic design of a resistor. Basically, a resistor limits the menstruation of accuse in a circuit and is an ohmic device where $V=IR$ . Most circuits have more than than one resistor. If several resistors are connected together and connected to a bombardment, the current supplied by the battery depends on the equivalent resistance of the circuit.

The equivalent resistance of a combination of resistors depends on both their individual values and how they are connected. The simplest combinations of resistors are series and parallel connections (Figure six.2.i). In a series circuit , the output current of the first resistor flows into the input of the 2nd resistor; therefore, the electric current is the aforementioned in each resistor. In a parallel circuit , all of the resistor leads on one side of the resistors are connected together and all the leads on the other side are connected together. In the case of a parallel configuration, each resistor has the aforementioned potential drop beyond it, and the currents through each resistor may be dissimilar, depending on the resistor. The sum of the individual currents equals the current that flows into the parallel connections.

(Figure half-dozen.2.1) $\begin{gather*}.\end{gather*}$

Par a shows four resistors connected in series and part b shows four resistors connected in parallel. — **Figure six.2.one** (a) For a series connexion of resistors, the current is the same in each resistor. (b) For a parallel connectedness of resistors, the voltage is the same beyond each resistor.

Resistors in Serial

Resistors are said to be in series whenever the current flows through the resistors sequentially. Consider Figure 6.2.2, which shows three resistors in serial with an applied voltage equal to $V_{ab}$ . Since there is just ane path for the charges to menses through, the current is the aforementioned through each resistor. The equivalent resistance of a set of resistors in a series connection is equal to the algebraic sum of the individual resistances.

(Figure 6.2.2) $\begin{gather*}.\end{gather*}$

Part a shows original circuit with three resistors connected in series to a voltage source and part b shows the equivalent circuit with one equivalent resistor connected to the voltage source. — Figure half dozen.2.ii (a) 3 resistors continued in series to a voltage source. (b) The original circuit is reduced to an equivalent resistance and a voltage source.

In Figure 6.2.two, the current coming from the voltage source flows through each resistor, then the current through each resistor is the same. The electric current through the circuit depends on the voltage supplied past the voltage source and the resistance of the resistors. For each resistor, a potential drib occurs that is equal to the loss of electric potential free energy as a current travels through each resistor. According to Ohm'due south law, the potential driblet $V$ across a resistor when a current flows through it is calculated using the equation $V=IR$ , where $I$ is the current in amps ( $\mathrm{A}$ ) and $R$ is the resistance in ohms ( $\Omega$ ). Since energy is conserved, and the voltage is equal to the potential free energy per charge, the sum of the voltage practical to the circuit by the source and the potential drops across the individual resistors around a loop should exist equal to zilch:

$\sum_{i=1}^{N}V_i=0.$

This equation is often referred to every bit Kirchhoff'southward loop law, which nosotros volition look at in more particular later in this chapter. For Figure 6.2.2 , the sum of the potential drop of each resistor and the voltage supplied by the voltage source should equal zero:

$\begin{eqnarray*}V-V_1-V_2-V_3&=&0,\\\Rightarrow V&=&V_1+V_2+V_3\\&=&IR_1+IR_2+IR_3,\\\Rightarrow I&=&\frac{V}{R_1+R_2+R_3}=\frac{V}{R_{\mathrm{eq}}}.\end{eqnarray*}$

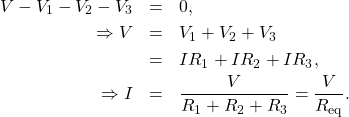
Since the current through each component is the same, the equality can be simplified to an equivalent resistance, which is just the sum of the resistances of the individual resistors.

Whatsoever number of resistors tin can exist connected in series. If $N$ resistors are connected in series, the equivalent resistance is

(6.ii.1) 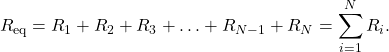$\begin{equation*}R_{\mathrm{eq}}=R_1+R_2+R_3+\ldots+R_{N-1}+R_N=\sum_{i=1}^NR_i.\end{equation*}$

One effect of components connected in a serial circuit is that if something happens to 1 component, information technology affects all the other components. For example, if several lamps are connected in serial and i bulb burns out, all the other lamps go nighttime.

EXAMPLE 6.2.1

Equivalent Resistance, Current, and Power in a Serial Circuit

A bombardment with a terminal voltage of $9~\mathrm{V}$ is connected to a circuit consisting of four $20{\text -}\Omega$ and ane $10{\text -}\Omega$ resistors all in series (Figure 6.two.3). Assume the battery has negligible internal resistance. (a) Calculate the equivalent resistance of the circuit. (b) Calculate the current through each resistor. (c) Calculate the potential drib across each resistor. (d) Decide the total ability dissipated by the resistors and the power supplied by the battery.

(Figure half-dozen.two.3) $\begin{gather*}.\end{gather*}$

The figure shows four resistors of 20 Ω and one resistor of 10 Ω connected in series to a 9 V voltage source. — Figure 6.2.three A simple series circuit with five resistors.

Strategy

In a series circuit, the equivalent resistance is the algebraic sum of the resistances. The current through the circuit can exist establish from Ohm's law and is equal to the voltage divided by the equivalent resistance. The potential drop across each resistor can be found using Ohm's law. The power prodigal by each resistor can be found using $P=I^2R$ , and the total power dissipated by the resistors is equal to the sum of the ability prodigal by each resistor. The power supplied past the battery can be found using $P=I\mathcal{E}$ .

Solution

a. The equivalent resistance is the algebraic sum of the resistances:

$R_{\mathrm{eq}}=R_1+R_2+R_3+R_4+R_5=20~\Omega+20~\Omega+20~\Omega+20~\Omega+10~\Omega=90~\Omega$

b. The current through the circuit is the same for each resistor in a series circuit and is equal to the applied voltage divided by the equivalent resistance:

$I=\frac{V}{R_{\mathrm{eq}}}=\frac{9~\mathrm{V}}{90~\Omega}=0.1~\mathrm{A}.$

c. The potential drop across each resistor can exist establish using Ohm'south police force:

$V_1=V_2=V_3=V_4=(0.1~\mathrm{A})20~\Omega=2~\mathrm{V},$

$V_5=(0.1~\mathrm{A})10~\Omega=1~\mathrm{V},$

$V_1+V_2+V_3+V_4+V_5=9~\mathrm{V}.$

Annotation that the sum of the potential drops across each resistor is equal to the voltage supplied past the battery.

d. The ability prodigal by a resistor is equal to $P=I^2R$ , and the ability supplied by the battery is equal to $P=I\mathcal{E}$ :

$P_1=P_2=P_3=P_4=(0.1~\mathrm{A})^2(20~\Omega)=0.2~\mathrm{W},$

$P_5=(0.1~\mathrm{A})^2(10~\Omega)=0.1~\mathrm{W},$

$P_{\mathrm{dissipated}}=0.2~\mathrm{W}+0.2~\mathrm{W}+0.2~\mathrm{W}+0.2~\mathrm{W}+0.1~\mathrm{W}=0.9~\mathrm{W},$

$P_{\mathrm{source}}=I\mathcal{E}=(0.1~\mathrm{A})(9~\mathrm{V})=0.9~\mathrm{W}.$

Significance

There are several reasons why we would apply multiple resistors instead of just one resistor with a resistance equal to the equivalent resistance of the circuit. Perhaps a resistor of the required size is not available, or nosotros need to dissipate the rut generated, or we want to minimize the toll of resistors. Each resistor may cost a few cents to a few dollars, just when multiplied by thousands of units, the cost saving may be appreciable.

Cheque YOUR UNDERSTANDING 6.2

Some strings of miniature holiday lights are made to brusk out when a bulb burns out. The device that causes the brusque is called a shunt, which allows current to catamenia around the open circuit. A "short" is like putting a piece of wire across the component. The bulbs are ordinarily grouped in series of 9 bulbs. If too many bulbs burn out, the shunts eventually open. What causes this?

Let's briefly summarize the major features of resistors in series:

Serial resistances add together to get the equivalent resistance:
$R_{\mathrm{eq}}=R_1+R_2+R_3+\ldots+R_{N-1}+R_N=\sum_{i=1}^NR_i.$
The same current flows through each resistor in series.
Individual resistors in serial do non get the total source voltage, simply divide it. The total potential drop across a series configuration of resistors is equal to the sum of the potential drops across each resistor.

Resistors in Parallel

Figure 6.2.4shows resistors in parallel, wired to a voltage source. Resistors are in parallel when one end of all the resistors are connected by a continuous wire of negligible resistance and the other stop of all the resistors are too connected to i some other through a continuous wire of negligible resistance. The potential drib beyond each resistor is the same. Electric current through each resistor can be plant using Ohm's law $I=V/R$ , where the voltage is abiding across each resistor. For example, an car'southward headlights, radio, and other systems are wired in parallel, so that each subsystem utilizes the full voltage of the source and can operate completely independently. The same is true of the wiring in your business firm or any building.

(Figure vi.2.4) $\begin{gather*}.\end{gather*}$

Part a shows original circuit with two resistors connected in parallel to a voltage source and part b shows the equivalent circuit with one equivalent resistor connected to the voltage source. — **Effigy 6.2.4** (a) Two resistors connected in parallel to a voltage source. (b) The original circuit is reduced to an equivalent resistance and a voltage source.

The electric current flowing from the voltage source in Figure 6.ii.four depends on the voltage supplied by the voltage source and the equivalent resistance of the circuit. In this case, the current flows from the voltage source and enters a junction, or node, where the circuit splits flowing through resistors $R_1$ and $R_2$ . As the charges flow from the battery, some get through resistor $R_1$ and some flow through resistor $R_2$ . The sum of the currents flowing into a junction must be equal to the sum of the currents flowing out of the junction:

$\sum I_{\mathrm{in}}=\sum I_{\mathrm{out}}.$

This equation is referred to equally Kirchhoff'due south junction rule and will be discussed in detail in the next department. In Figure 6.two.4, the junction rule gives $I=I_1+I_2$ . In that location are two loops in this circuit, which leads to the equations $V=I_1R_1$ and $I_1R_1=I_2R_2$ Note the voltage across the resistors in parallel are the same ( $V=V_1=V_2$ ) and the current is additive:

$\begin{eqnarray*}I&=&I_1+I_2\\&=&\frac{V_1}{R_1}+\frac{V_2}{R_2}\\&=&\frac{V}{R_1}+\frac{V}{R_2}\\&=&V\left(\frac{1}{R_1}+\frac{1}{R_2}\right)=\frac{V}{R_{\mathrm{eq}}}\\\Rightarrow R_{\mathrm{eq}}&=&\left(\frac{1}{R_1}+\frac{1}{R_2}\right)^{-1}.\end{eqnarray*}$

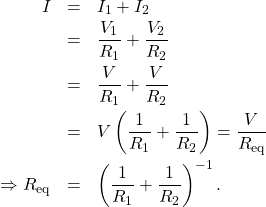
Generalizing to any number of $N$ resistors, the equivalent resistance $R_{\mathrm{eq}}$ of a parallel connection is related to the individual resistances by

(6.2.ii) 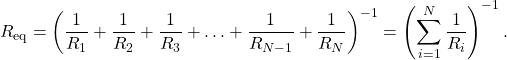$\begin{equation*}R_{\mathrm{eq}}&=&\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\ldots+\frac{1}{R_{N-1}}+\frac{1}{R_N}\right)^{-1}=\left(\sum_{i=1}^N\frac{1}{R_i}\right)^{-1}.\end{equation*}$

This relationship results in an equivalent resistance $R_{\mathrm{eq}}$ that is less than the smallest of the private resistances. When resistors are connected in parallel, more electric current flows from the source than would menses for any of them individually, so the total resistance is lower.

Example 6.two.2

Analysis of a Parallel Excursion

Three resistors $R_1=1.00~\Omega$ , $R_2=2.00~\Omega$ , and $R_3=2.00~\Omega$ are connected in parallel. The parallel connexion is fastened to a $V=3.00~\mathrm{V}$ voltage source. (a) What is the equivalent resistance? (b) Detect the electric current supplied by the source to the parallel circuit. (c) Calculate the currents in each resistor and testify that these add together to equal the current output of the source. (d) Summate the power prodigal past each resistor. (e) Find the power output of the source and show that it equals the total power dissipated by the resistors.

Strategy

(a) The total resistance for a parallel combination of resistors is found using $R_{\mathrm{eq}}=\left(\sum_{i=1}^N\frac{1}{R_i}\right)^{-1}$ .
(Note that in these calculations, each intermediate answer is shown with an extra digit.)

(b) The current supplied by the source can be found from Ohm's law, substituting $R_{\mathrm{eq}}$ for the total resistance $I=\frac{V}{R_{\mathrm{eq}}}$ .

(c) The private currents are easily calculated from Ohm's police force $\left(I_i=\frac{V_i}{R_i}\right)$ , since each resistor gets the full voltage. The total current is the sum of the individual currents: $I=\sum_iI_i$ .

(d) The power dissipated by each resistor tin can exist found using any of the equations relating power to current, voltage, and resistance, since all 3 are known. Let u.s.a. utilise $P_i=V^2/R_i$ , since each resistor gets full voltage.

(eastward) The total ability can also be calculated in several ways, utilize $P=IV$ .

Solution

a. The total resistance for a parallel combination of resistors is plant using Equation 6.2.ii. Inbound known values gives

$R_{\mathrm{eq}}&=&\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)^{-1}=\left(\frac{1}{1.00~\Omega}+\frac{1}{2.00~\Omega}+\frac{1}{2.00~\Omega}\right)^{-1}=0.50~\Omega.$

The full resistance with the correct number of meaning digits is $R_{\mathrm{eq}}=0.50~\Omega$ . As predicted, $R_{\mathrm{eq}}$ is less than the smallest private resistance.

b. The total current can exist found from Ohm'southward law, substituting $R_{\mathrm{eq}}$ for the full resistance. This gives

$I=\frac{V}{R_{\mathrm{eq}}}=\frac{3.00~\mathrm{V}}{0.50~\Omega}=6.00~\mathrm{A}.$

Current $I$ for each device is much larger than for the same devices continued in series (see the previous example). A circuit with parallel connections has a smaller total resistance than the resistors continued in series.

c. The individual currents are easily calculated from Ohm's law, since each resistor gets the total voltage. Thus,

$I_1=\frac{V}{R_1}=\frac{3.00~\mathrm{V}}{1.00~\Omega}=3.00~\mathrm{A}.$

Similarly,

$I_2=\frac{V}{R_2}=\frac{3.00~\mathrm{V}}{2.00~\Omega}=1.50~\mathrm{A}.$

and

$I_3=\frac{V}{R_3}=\frac{3.00~\mathrm{V}}{2.00~\Omega}=1.50~\mathrm{A}.$

The total electric current is the sum of the private currents:

$I_1+I_2+I_3=6.00~\mathrm{A}.$

d. The ability dissipated past each resistor can be found using whatever of the equations relating ability to current, voltage, and resistance, since all iii are known. Let usa apply $P=V^2/R$ , since each resistor gets full voltage. Thus,

$P_1=\frac{V^2}{R_1}=\frac{(3.00~\mathrm{V})^2}{1.00~\Omega}=9.00~\mathrm{W}.$

Similarly,

$P_2=\frac{V^2}{R_2}=\frac{(3.00~\mathrm{V})^2}{2.00~\Omega}=4.50~\mathrm{W}.$

and

$P_3=\frac{V^2}{R_3}=\frac{(3.00~\mathrm{V})^2}{2.00~\Omega}=4.50~\mathrm{W}.$

eastward. The total power can also be calculated in several ways. Choosing $P=IV$ and inbound the full current yields

$P=IV=(6.00~\mathrm{A})(3.00~\mathrm{V})=18.00~\mathrm{W}.$

Significance

Total ability dissipated past the resistors is also $18.00~\mathrm{W}$ :

$P_1+P_2+P_3=9.00~\mathrm{W}+4.50~\mathrm{W}+4.50~\mathrm{W}=18.00~\mathrm{W}$

Notice that the total power dissipated by the resistors equals the power supplied by the source.

Check YOUR Agreement half-dozen .three

Consider the same potential departure $(V=3.00~\mathrm{V})$ applied to the same three resistors connected in series. Would the equivalent resistance of the series circuit be higher, lower, or equal to the three resistor in parallel? Would the current through the serial circuit be higher, lower, or equal to the electric current provided past the same voltage applied to the parallel circuit? How would the power prodigal by the resistor in series compare to the ability dissipated past the resistors in parallel?

Check YOUR UNDERSTANDING vi.4

How would you use a river and two waterfalls to model a parallel configuration of two resistors? How does this analogy break downward?

Let us summarize the major features of resistors in parallel:

Equivalent resistance is found from
$R_{\mathrm{eq}}&=&\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\ldots+\frac{1}{R_{N-1}}+\frac{1}{R_N}\right)^{-1}=\left(\sum_{i=1}^N\frac{1}{R_i}\right)^{-1},$

and is smaller than any individual resistance in the combination.
The potential drop across each resistor in parallel is the same.
Parallel resistors exercise not each get the full current; they separate it. The electric current inbound a parallel combination of resistors is equal to the sum of the electric current through each resistor in parallel.

In this chapter, we introduced the equivalent resistance of resistors connect in series and resistors connected in parallel. You lot may call up that in Capacitance, we introduced the equivalent capacitance of capacitors continued in series and parallel. Circuits often contain both capacitors and resistors. Table 6.2.1 summarizes the equations used for the equivalent resistance and equivalent capacitance for series and parallel connections.

(Table 6.2.1) $\begin{gather*}.\end{gather*}$

Combinations of Series and Parallel

More circuitous connections of resistors are ofttimes just combinations of serial and parallel connections. Such combinations are mutual, peculiarly when wire resistance is considered. In that case, wire resistance is in series with other resistances that are in parallel.

Combinations of series and parallel tin can exist reduced to a single equivalent resistance using the technique illustrated inFigure 6.2.5. Diverse parts tin be identified every bit either series or parallel connections, reduced to their equivalent resistances, and so further reduced until a single equivalent resistance is left. The process is more time consuming than difficult. Here, we note the equivalent resistance as $R_{\mathrm{eq}}$ .

(Effigy 6.2.v) $\begin{gather*}.\end{gather*}$

Notice that resistors $R_3$ and $R_4$ are in serial. They can exist combined into a single equivalent resistance. 1 method of keeping track of the process is to include the resistors equally subscripts. Hither the equivalent resistance of $R_3$ and $R_4$ is

$R_{34}=R_3+R_4=6~\Omega+4~\Omega=10~\Omega.$

The excursion now reduces to 3 resistors, shown in Figure 6.2.5(c). Redrawing, we at present meet that resistors $R_2$ and $R_{34}$ found a parallel circuit. Those two resistors tin can exist reduced to an equivalent resistance:

$R_{234}=\left(\frac{1}{R_2}+\frac{1}{R_{34}}\right)^{-1}=\left(\frac{1}{10~\Omega}+\frac{1}{10~\Omega}\right)^{-1}=5~\Omega.$

This step of the process reduces the circuit to two resistors, shown in in Effigy vi.2.5 (d). Here, the circuit reduces to two resistors, which in this case are in series. These two resistors tin can be reduced to an equivalent resistance, which is the equivalent resistance of the circuit:

$R_{\mathrm{eq}}=R_{1234}=R_1+R_{234}=7~\Omega+5~\Omega=12~\Omega.$

The main goal of this excursion analysis is reached, and the circuit is now reduced to a single resistor and single voltage source.

Now nosotros can clarify the excursion. The current provided past the voltage source is $I=\frac{V}{R_{\mathrm{eq}}}=\frac{24~\mathrm{V}}{12~\Omega}=2~\mathrm{A}$ . This current runs through resistor $R_1$ and is designated as $I_1$ . The potential driblet across $R_1$ can exist institute using Ohm's law:

$V_1=I_1R_1=(2~\mathrm{A})(7~\Omega)=14~\mathrm{V}.$

Looking at Figure 6.2.5(c), this leaves $24~\mathrm{V}-14~\mathrm{V}=10~\mathrm{V}$ to be dropped beyond the parallel combination of $R_2$ and $R_{34}$ . The electric current through $R_2$ can be constitute using Ohm'due south constabulary:

$I_2=\frac{V_2}{R_2}=\frac{10~\mathrm{V}}{10~\Omega}=1~\mathrm{A}.$

The resistors $R_3$ and $R_4$ are in serial so the currents $I_3$ and $I_4$ are equal to

$I_3=I_4=I-I_2=2~\mathrm{A}-1~\mathrm{A}=1~\mathrm{A}.$

Using Ohm's law, nosotros can discover the potential drop beyond the last two resistors. The potential drops are $V_3=I_3R_3=6~\mathrm{V}$ and $V_4=I_4R_4=4~\mathrm{V}$ . The terminal analysis is to expect at the power supplied by the voltage source and the power dissipated past the resistors. The ability dissipated by the resistors is

$\begin{eqnarray*}P_1&=&I_1^2R_1=(2~\mathrm{A})^2(7~\Omega)=28~\mathrm{W},\\P_2&=&I_2^2R_2=(1~\mathrm{A})^2(10~\Omega)=10~\mathrm{W},\\P_3&=&I_3^2R_3=(1~\mathrm{A})^2(6~\Omega)=6~\mathrm{W},\\P_4&=&I_4^2R_4=(1~\mathrm{A})^2(4~\Omega)=4~\mathrm{W},\\P_{\mathrm{dissipated}}&=&P_1+P_2+P_3+P_4=48~\mathrm{W}.\end{eqnarray*}$

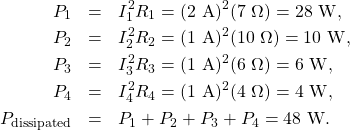
The total free energy is constant in any process. Therefore, the power supplied by the voltage source is $P_s=IV=(2~\mathrm{A})(24~\mathrm{V})=48~\mathrm{W}$ . Analyzing the power supplied to the circuit and the ability dissipated by the resistors is a good check for the validity of the analysis; they should exist equal.

Example half dozen.2.3

Combining Serial and Parallel Circuits

Figure half-dozen.two.half-dozen shows resistors wired in a combination of serial and parallel. We can consider $R_1$ to be the resistance of wires leading to $R_2$ and $R_3$ (a) Find the equivalent resistance of the circuit. (b) What is the potential drop $V_1$ across resistor $R_1$ ? (c) Find the current $I_2$ through resistor $R_2$ . (d) What ability is dissipated by $R_2$ ?

(Figure 6.2.6) $\begin{gather*}.\end{gather*}$

Strategy

(a) To observe the equivalent resistance, first find the equivalent resistance of the parallel connection of $R_2$ and $R_3$ . So use this result to observe the equivalent resistance of the serial connection with $R_1$ .

(b) The electric current through $R_1$ can exist found using Ohm's police force and the voltage applied. The current through $R_1$ is equal to the current from the bombardment. The potential drop $V_1$ across the resistor $R_1$ (which represents the resistance in the connecting wires) can exist plant using Ohm'south law.

(c) The current through $R_2$ tin can be plant using Ohm's constabulary $I_2=\frac{V_2}{R_2}$ . The voltage across $R_2$ tin can be institute using $V_2=V-V_1$ .

(d) Using Ohm's constabulary $(V_2=I_2R_2)$ , the ability dissipated past the resistor can also be establish using $P_2=I_2^2R_2=\frac{V_2^2}{R_2}$ .

Solution

a. To find the equivalent resistance of the circuit, notice that the parallel connection of R 2 R2 and R 3 R3 is in series with R 1 R1 , so the equivalent resistance is

$R_{\mathrm{eq}}=R_1+\left(\frac{1}{R_2}+\frac{1}{R_3}\right)^{-1}=1.00~\Omega+\left(\frac{1}{6.00~\Omega}+\frac{1}{13.00~\Omega}\right)^{-1}=5.10~\Omega.$

The full resistance of this combination is intermediate between the pure series and pure parallel values ( $20.0~\Omega$ and $0.804~\Omega$ , respectively).

b. The electric current through $R_1$ is equal to the current supplied past the battery:

$I_1=I=\frac{V}{R_{\mathrm{eq}}}=\frac{12.0~\mathrm{V}}{5.10~\Omega}=2.35~\mathrm{A}.$

The voltage across $R_1$ is

$V_1=I_1R_1=(2.35~\mathrm{A})(1~\Omega)=2.35~\mathrm{V}.$

The voltage applied to $R_2$ and $R_3$ is less than the voltage supplied past the battery by an amount $V_1$ . When wire resistance is big, information technology tin significantly bear upon the performance of the devices represented past $R_2$ and $R_3$ .

c. To find the current through $R_2$ , we must commencement find the voltage applied to it. The voltage across the ii resistors in parallel is the same:

$V_2=V_3=V-V_1=12.0~\mathrm{V}-2.35~\mathrm{V}=9.65~\mathrm{V}.$

Now we can find the current $I_2$ through resistance $R_2$ using Ohm'southward police:

$I_2=\frac{V_2}{R_2}=\frac{9.65~\mathrm{V}}{6.00~\Omega}=1.61~\mathrm{A}.$

The current is less than the $2.00~\mathrm{A}$ that flowed through $R_2$ when it was connected in parallel to the battery in the previous parallel circuit case.

d. The ability dissipated by $R_2$ is given by

$P_2=I_2^2R_2=(1.61~\mathrm{A})^2(6.00~\Omega)=15.5~\mathrm{W}.$

Significance

The analysis of complex circuits can frequently be simplified past reducing the circuit to a voltage source and an equivalent resistance. Even if the entire circuit cannot be reduced to a single voltage source and a single equivalent resistance, portions of the circuit may be reduced, greatly simplifying the analysis.

Bank check YOUR UNDERSTANDING 6.5

Consider the electrical circuits in your domicile. Give at least ii examples of circuits that must employ a combination of series and parallel circuits to operate efficiently.

Practical Implications

One implication of this last example is that resistance in wires reduces the electric current and power delivered to a resistor. If wire resistance is relatively large, equally in a worn (or a very long) extension cord, then this loss can be meaning. If a large current is drawn, the $IR$ drop in the wires can also be significant and may become apparent from the rut generated in the cord.

For case, when y'all are rummaging in the fridge and the motor comes on, the fridge light dims momentarily. Similarly, you lot tin see the passenger compartment light dim when you lot start the engine of your car (although this may be due to resistance inside the battery itself).

What is happening in these high-current situations is illustrated in Figure six.ii.7. The device represented past $R_3$ has a very low resistance, so when it is switched on, a large current flows. This increased current causes a larger $IR$ drop in the wires represented by $R_1$ , reducing the voltage across the low-cal bulb (which is $R_2$ ), which then dims noticeably.

(Figure 6.2.7) $\begin{gather*}.\end{gather*}$

Problem-Solving Strategy: Series and Parallel Resistors

Draw a clear excursion diagram, labeling all resistors and voltage sources. This stride includes a list of the known values for the problem, since they are labeled in your circuit diagram.
Identify exactly what needs to be adamant in the problem (place the unknowns). A written listing is useful.
Make up one's mind whether resistors are in series, parallel, or a combination of both series and parallel. Examine the circuit diagram to brand this assessment. Resistors are in series if the same current must laissez passer sequentially through them.
Employ the appropriate list of major features for series or parallel connections to solve for the unknowns. There is ane listing for serial and another for parallel.
Check to run into whether the answers are reasonable and consequent.

Case 6.ii.4

Combining Series and Parallel Circuits

2 resistors connected in series $(R_1,R_2)$ are connected to two resistors that are connected in parallel $(R_3,R_4)$ . The series-parallel combination is connected to a battery. Each resistor has a resistance of $10.00~\Omega$ . The wires connecting the resistors and battery have negligible resistance. A current of $2.00~\mathrm{A}$ runs through resistor $R_1$ . What is the voltage supplied by the voltage source?

Strategy

Use the steps in the preceding problem-solving strategy to detect the solution for this example.

Solution

Describe a articulate circuit diagram (Figure half-dozen.two.viii).

(Effigy half dozen.two.viii) $\begin{gather*}.\end{gather*}$

Figure 6.ii.8 To find the unknown voltage, nosotros must get-go find the equivalent resistance of the excursion.
The unknown is the voltage of the battery. In order to find the voltage supplied by the battery, the equivalent resistance must be found.
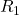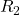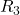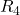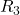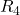In this excursion, nosotros already know that the resistors $R_1$ and $R_2$ are in series and the resistors $R_3$ and $R_4$ are in parallel. The equivalent resistance of the parallel configuration of the resistors $R_3$ and $R_4$ is in series with the series configuration of resistors 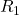$R_1$ and $R_2$ .
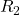The voltage supplied past the battery tin can exist plant by multiplying the current from the battery and the equivalent resistance of the excursion. The current from the bombardment is equal to the electric current through 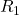$R_1$ and is equal to 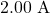$2.00~\mathrm{A}$ . We need to discover the equivalent resistance by reducing the circuit. To reduce the circuit, offset consider the 2 resistors in parallel. The equivalent resistance is 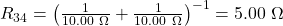$R_{34}=\left(\frac{1}{10.00~\Omega}+\frac{1}{10.00~\Omega}\right)^{-1}=5.00~\Omega$ . This parallel combination is in series with the other 2 resistors, so the equivalent resistance of the circuit is 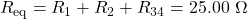$R_{\mathrm{eq}}=R_1+R_2+R_{34}=25.00~\Omega$ . The voltage supplied by the battery is therefore $V=IR_{\mathrm{eq}}=2.00~\mathrm{A}(25.00~\Omega)=50.0~\mathrm{V}$ .
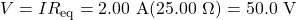Ane way to check the consistency of your results is to calculate the power supplied past the bombardment and the power prodigal by the resistors. The power supplied by the battery is
$P_{\mathrm{batt}}=IV=100.00~\mathrm{W}.$

Since they are in series, the current through 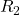$R_2$ equals the electric current through 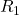$R_1$ . Since 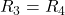$R_3=R_4$ , the current through each will be 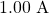$1.00~\mathrm{A}$ . The ability dissipated by the resistors is equal to the sum of the power dissipated by each resistor:

$\begin{eqnarray*}P&=&I_1^2R_1+I_2^2R_2+I_3^2R_3+I_4^2R_4\\&=&40.00~\mathrm{W}+40.00~\mathrm{W}+10.00~\mathrm{W}+10.00~\mathrm{W}\\&=&100.00~\mathrm{W}.\end{eqnarray*}$

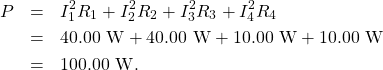
Since the power dissipated by the resistors equals the power supplied past the battery, our solution seems consistent.

Significance

If a problem has a combination of serial and parallel, as in this example, information technology can exist reduced in steps by using the preceding problem-solving strategy and by considering individual groups of series or parallel connections. When finding $R_{\mathrm{eq}}$ for a parallel connectedness, the reciprocal must be taken with intendance. In addition, units and numerical results must be reasonable. Equivalent serial resistance should exist greater, whereas equivalent parallel resistance should be smaller, for example. Ability should be greater for the same devices in parallel compared with series, and so on.