how to find standard deviation of a sample
What is Standard Deviation?
Standard deviation is a term which measures the amount of variation or dispersion of a set of values. If the values are shut to the hateful of the set, it volition exist a depression standard divergence. If the values are spread in a wider range, it will be a high standard deviation.
The concept of standard deviation was presented past KarI Pearson in 18th century. Standard deviation is the measurement of variation between given values in a grouping. SD is e'er calculated from the arithmetic hateful non from median or manner. It is denoted past the symbol of sigma (σ)
Standard Divergence formula
The standard difference formula for population is:
$$SD=σ=\sqrt\frac{\sum(x-µ)^2}{n}$$
In the standard deviation formula the ∑ means summation value of the ascertainment. x is value in the given data fix and µ is the hateful of the given information set of the population and northward means the total number of items.
For every data fix the sample standard divergence formula will exist:
$$SD=σ=\sqrt\frac{\sum(ten-x)^-ii}{n-i}$$
Use summation figurer and expected variance figurer to acquire the calculations of summation and variance.
How to calculate standard divergence?
Follow below steps to calculate standard deviation stride by pace:
Step #1: Detect out the mean (µ) of the given data.
Step #2: Decrease the mean (µ) from each given value (divergence from the mean).
Pace #three: Have foursquare of the each deviation of the hateful.
Footstep #4: Find out the summation of the taken squares.
Footstep #5: Divide its total past the number (due north) which volition exist chosen variance.
Step #6: Take the square root of variance, the result will be called the standard difference.
Standard deviation estimator works in the same manner every bit given to a higher place. You can besides discover other useful calculators similar integration calculator and differentiation computer for free.
How to find Standard Deviation?
In order to learn how to find standard divergence lets solve an example.
The math test scores of different students are: 91, 91, 91, 41, 51.
To discover standard deviation of the given class we will use standard departure formula.
$$SD= σ =\sqrt\frac{\sum(x-µ)^2}{n}$$
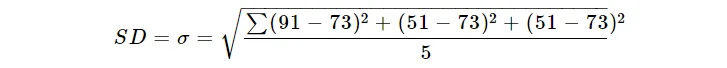
$$\sqrt\frac{\sum(eighteen+18+xviii-32-22)^ii}{n}$$
$$\sqrt\frac{324+324+324+1024+484}{5}$$
$$\sqrt\frac{2480}{v}$$
$$SD= σ =\sqrt496$$
$$SD= σ =22.27105745132$$
Below steps will help u.s.a. finding standard deviation
Footstep #1: Find the mean K
(91 + 91 + 91 + 41 + 51) / five = 73
Step #2: Calculate the deviation from the hateful
91 – 73 = 18, 91 – 73 = 18, 91 – 73 = xviii, 41 – 73 = -32, 51 – 73 = -22
Stride #3: Square of each deviation from the mean
(18)² = 324, (18)² = 324, (18)² = 324, (-32)² = 1,024, (-22)² = 484
Step #4: Summate the sum of all squares
324 + 324 + 324 + 1,024 + 484 = 2,480
Stride #5: Divide the total of the taken squares by the number of items (n)
two,480 / 5 = 496
Pace #six: Find the square root of the variance
$$\sqrt496=22$$
Standard deviation as well helps to larn the concepts of quadratics and trapezoid. For the calculations, yous can use our quadratic formula calculator and trapezoid surface area computer.
How to summate Standard Deviation of the class?

Let's say a physics class took a test with scores of 90, 90, ninety, l, fifty and we are to calculate the standard deviation for the class.
$$SD= σ =\sqrt\frac{\sum(10-µ)^ii}{north}$$
$$SD= σ^2 =\frac{\sum(10-µ)^2}{due north}$$
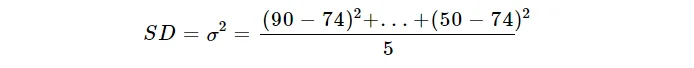
$$=\frac{1920}{five}$$
$$=384$$
$$=\sqrt384$$
$$=19.595917942265$$
Our portal likewise has log figurer and antilog calculator for students and teachers. Yous can larn about the formulas, equations and calculations of logarithm and antilogarithm on our website for free.
What is Standard Fault?
The sample hateful differs from the bodily hateful of population's data fix; this deviation is chosen standard mistake of the mean. Standard error occures when nosotros collect minor sample data or too much samples of population, the variation causes departure among set of values.
Standard Difference vs Standard Mistake
Standard deviation differs from standard error. Standard difference tells the amount of variability and dispersion from the hateful of data. Standard fault tells virtually the divergence between the sample mean and true population hateful.
Standard error of mean is ever smaller than standard deviation. Standard error calculator calculates the standard difference equation and finds the standard error (SE).
Click on to learn how to detect arc length and how to multiply vectors.
Standard Mistake formula
Standard error formula to summate standard error is
$$SE=\frac{σ }{\sqrt(due north)}$$
Standard mistake is helpful for yous to accurate the mean of given data from that specific population which likely would exist compared to the actual population mean.
Standard Deviation between two sets of data
Standard deviation finds the differenence in numbers and diverseness of the data prepare values.
If the data is 3, 7, vii, 19 vs 2, five, half-dozen, vii. Follow beneath steps to summate SD between 2 sets of data. The steps are
Footstep #1: Collect information to create information set to calculate the standard departure.
Stride #2: Calculate the average and mean of data set by adding all the numbers and dividing the total past the number of items in data set.
(3 + 7 + 7 + xix) / 4 = nine vs (2 + 5 + vi + vii) / 4 = five
Hither the mean is 5
Step #iii: Subtract the mean from the first number in your data prepare and square the differences.
three – 9 = -6² = 36, 7 – 9 = -2² = 4, 7 – 9 = -2² = 4, nineteen – 9 = x² = 100
Vs
two – 5 = -iii² = 9, 5 – 5 = 0² = 0, 6 – 5 = i² = 1 7 – 5 = two² = 4
Stride #four: Add squared differences and separate the total by the number of items in data prepare.
36 + 4 + 4 +100 = 144
144 / 4 = 36
Vs
9 + 1 + 4 = 14
Step #5: Take the square root of this mean of differences to find the standard deviation.
$$\sqrt36=vi$$
Vs
$$\sqrt14=3.74$$
This is how we calculate the standard departure between two sets of information.
In society to consolidate your concepts regarding divergence of numbers, yous can do midpoint and rounding using midpoint estimator and best rounding calculator.
What is Standard Divergence Calculator?
Like other math concepts, finding standard deviation tin can be difficult if we do not have its proper concept. Calculatored has introduced an online Standard difference computer which takes the input and provides authentic results instantly.
How to use Standard Deviation Reckoner?
Standard deviation reckoner is fast, accurate and free to use. Yous only need to enter the values of data set up and our free standard deviation calculator will instantly calculate the values of mean, standard divergence (SD) and variance.
With this majestic free standard deviation reckoner we as well offers limit calculator for your learning and calculations regarding limit functions.
Source: https://www.calculatored.com/math/calculus/standard-deviation-calculator
Posted by: greensupoed.blogspot.com

0 Response to "how to find standard deviation of a sample"
Post a Comment